SSCP Exam Results

L2F (Layer 2 Forwarding) provides no authentication or encryption. It is a Protocol that supports the creation of secure virtual private dial-up networks over the Internet.

At one point L2F was merged with PPTP to produce L2TP to be used on networks and not only on dial up links.

IPSec is now considered the best VPN solution for IP environments.

Source: HARRIS, Shon, All-In-One CISSP Certification Exam Guide, McGraw-Hill/Osborne, 2002, Chapter 8: Cryptography (page 507).

The following answers are incorrect.

Symmetric Key. Is incorrect because RSA is a Public Key or a Asymmetric Key cryptographic system and not a Symmetric Key or a Secret Key cryptographic system.

Secret Key. Is incorrect because RSA is a Public Key or a Asymmetric Key cryptographic system and not a Secret Key or a Symmetric Key cryptographic system.

Private Key. Is incorrect because Private Key is just one part if an Asymmetric Key cryptographic system, a Private Key used alone is also called a Symmetric Key cryptographic system.

Source: TIPTON, Hal, (ISC)2, Introduction to the CISSP Exam presentation.

An extremely simple example of conventional cryptography is a substitution cipher.

A substitution cipher substitutes one piece of information for another. This is most frequently done by offsetting letters of the alphabet. Two examples are Captain Midnight's Secret Decoder Ring, which you may have owned when you were a kid, and Julius Caesar's cipher. In both cases, the algorithm is to offset the alphabet and the key is the number of characters to offset it. So the offset could be one, two, or any number you wish. ROT-13 is an example where it is shifted 13 spaces. The Ceaser Cipher is another example where it is shifted 3 letters to the left.

ROT13 ("rotate by 13 places", sometimes hyphenated ROT-13) is a simple letter substitution cipher that replaces a letter with the letter 13 letters after it in the alphabet. ROT13 is an example of the Caesar cipher, developed in ancient Rome.

In the basic Latin alphabet, ROT13 is its own inverse; that is, to undo ROT13, the same algorithm is applied, so the same action can be used for encoding and decoding. The algorithm provides virtually no cryptographic security, and is often cited as a canonical example of weak encryption.

ROT13 is used in online forums as a means of hiding spoilers, puzzle solutions, and offensive materials from the casual glance. ROT13 has been described as the "Usenet equivalent of a magazine printing the answer to a quiz upside down". ROT13 has inspired a variety of letter and word games on-line, and is frequently mentioned in newsgroup conversations. See diagram Below:

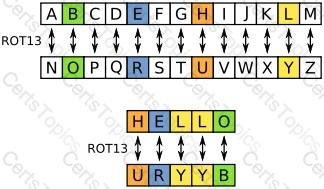
Rot 13 Cipher

The following are incorrect:

The Caesar cipher is a simple substitution cipher that involves shifting the alphabet three positions to the right. In cryptography, a Caesar cipher, also known as Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on. The method is named after Julius Caesar, who used it in his private correspondence.

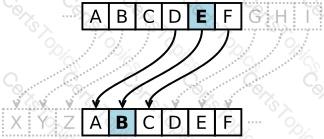
Caesar Cipher

Polyalphabetic cipher refers to using multiple alphabets at a time. A polyalphabetic cipher is any cipher based on substitution, using multiple substitution alphabets. The Vigenère cipher is probably the best-known example of a polyalphabetic cipher, though it is a simplified special case.

Viginere Cipher

Transposition cipher is a different type of cipher. In cryptography, a transposition cipher is a method of encryption by which the positions held by units of plaintext (which are commonly characters or groups of characters) are shifted according to a regular system, so that the ciphertext constitutes a permutation of the plaintext. That is, the order of the units is changed. See the reference below for multiple examples of Transpositio Ciphers.

An exemple of Transposition cipher could be columnar transposition, the message is written out in rows of a fixed length, and then read out again column by column, and the columns are chosen in some scrambled order. Both the width of the rows and the permutation of the columns are usually defined by a keyword. For example, the word ZEBRAS is of length 6 (so the rows are of length 6), and the permutation is defined by the alphabetical order of the letters in the keyword. In this case, the order would be "6 3 2 4 1 5".

In a regular columnar transposition cipher, any spare spaces are filled with nulls; in an irregular columnar transposition cipher, the spaces are left blank. Finally, the message is read off in columns, in the order specified by the keyword. For example, suppose we use the keyword ZEBRAS and the message WE ARE DISCOVERED. FLEE AT ONCE. In a regular columnar transposition, we write this into the grid as Follows:

Transposition Cipher

Providing five nulls (QKJEU) at the end. The ciphertext is then read off as:

EVLNE ACDTK ESEAQ ROFOJ DEECU WIREE

Reference(s) used for this question: