IFoA IFoA_CAA_M0 Dumps

A discrete random variable can only take the values 2,3,4 or 5. The probabilities associated with some of the outcomes are: P(X=2) = 0.2, P(X=3) = 0.3, P(X=5) = 0.1.

For a randomly drawn value of X, calculate P(X>3).

Consider a function f which has three variables, x1, x2 and x3.

Identify which of the following gives a correct definition of a partial derivative of the function f.

Three light bulbs are chosen at random from 15 bulbs of which 5 are known to be defective.

Calculate the probability that exactly one of the three is defective.

A)

B)

C)

D)

Let A = 

Let B =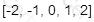 

Calculate   

Determine which of the options is equal to log(3) - 2log(x+1).

A)

B)

C)

D)

A recurrence relation is given by: Un = 2Un - 1 + 3

If U0 = 0, calculate U2 =  

The stem and leaf chart below shows the ages of all the pensioners in a small village.

Identify which of the following is not true.

For random variable X, use the following statistics to calculate its coefficient of skewness based on central moments.

E(X) = 3.940

E(X2) = 21.466

skew(X) = E[(X - μ)3] = 6.008

Identify which of the following statements are true.

I. Skewness measures how peaked a set of data is.

II. Skewness is a measure of asymmetry of the distribution of the data about its mean.

III. For a symmetrically distributed data, the mean equals the median but not necessarily the mode.

IV. The value of a measure of skewness can be positive, zero or negative.